Often you have a truck load of potential explanatory variables, that all might interact with each other, giving a multitude of potential ways the explanatory variables could relate to the dependent variable. You could painstakingly create every possible model or you could do a step-wise regression. Step-wise regression automatically adds and subtracts variables from your model and checks whether it improves the model using AIC as a selection criteria (AIC is a relative score of goodness).

Below is how I would do it. In this example we are trying to explain inflammation with a number of variables such as Age, Sex, Bacterial Count etc.

First Load the data and packages. Make sure the data makes sense (you should always do this),  e.g. are the numerical variables numerical?

#Load package
library(MASS)

#Load data
dat<- read.table(url("https://jackauty.com/wp-content/uploads/2020/05/Stepwise-regression-data.txt"),header=T)

#Check data, make sure it makes sense
str(dat)

'data.frame': 100 obs. of 8 variables:
 $ Inflammation : num 4.4 1218.07 5.32 3072.58 108.86 ...
 $ Age : num 7.16 8.88 3.23 7.91 7.98 2.93 9.12 9.41 7.71 2.91 ...
 $ Sex : Factor w/ 2 levels "F","M": 2 1 1 1 2 1 1 2 1 1 ...
 $ Blood.pressure : num 151 145 104 156 143 159 114 140 149 114 ...
 $ Infection : Factor w/ 2 levels "No","Yes": 1 2 1 2 1 1 1 1 2 1 ...
 $ Bacterial.count : num 75 5718 27 4439 224 ...
 $ Inflammation.transformed : num 2.1 34.9 2.31 55.43 10.43 ...
 $ inflammation.boxcox.transformed: num 2.43 71.02 2.73 123.74 16.68 ...

Next, check if the dependent variable is normally distributed. It doesn’t have to be, but things will go smoother if it is. In this example the dependent variable distribution was improved by a square-root transformation. So I created a new transformed variable.

#Check dependent variable, ideally it's normally distributed. Transform if need
hist(dat$Inflammation, breaks=6)



hist(sqrt(dat$Inflammation), breaks=6)


#Square root looks better, so let's create a variable to use in our model
dat$Inflammation.transformed<-sqrt(dat$Inflammation)

Next let’s build the full model. The full model is a model with all the explanatory variables interacting with each other! and then run a step-wise regression in both directions (stepping forward and backward)

#Set up full model
full.model<-lm(Inflammation.transformed ~ Age*Sex*Blood.pressure*Infection*Bacterial.count, data = dat)
summary(full.model)


#Full model is crazy (note red notes generated in paint :))

#Perform stepwise regression in both directions
step.model<-stepAIC(full.model, direction="both", trace = F)

summary(step.model)

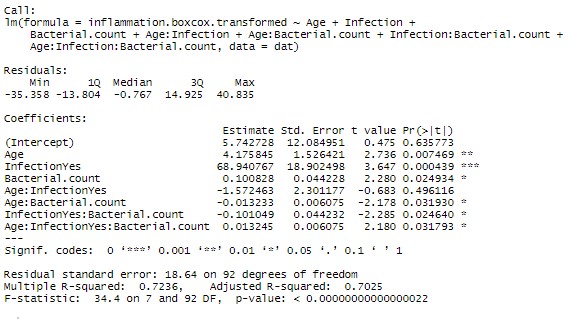
Now given the marginal significance of the three way interaction term, and the difficulty in interpreting three-way interaction terms, I’d be tempted to make a model without that term and check if there is a substantial difference in the model (using AIC or adjusted Rsquared). If the difference is minor, I’d go with the more parsimonious model.

One last step! Check that your residuals are heteroskedastic, normally distributed and there are no major outliers.

#Make it so you can see four graphs in one plot area
par(mfrow=c(2,2)) 

#Plot your assumption graphs
plot(step.model)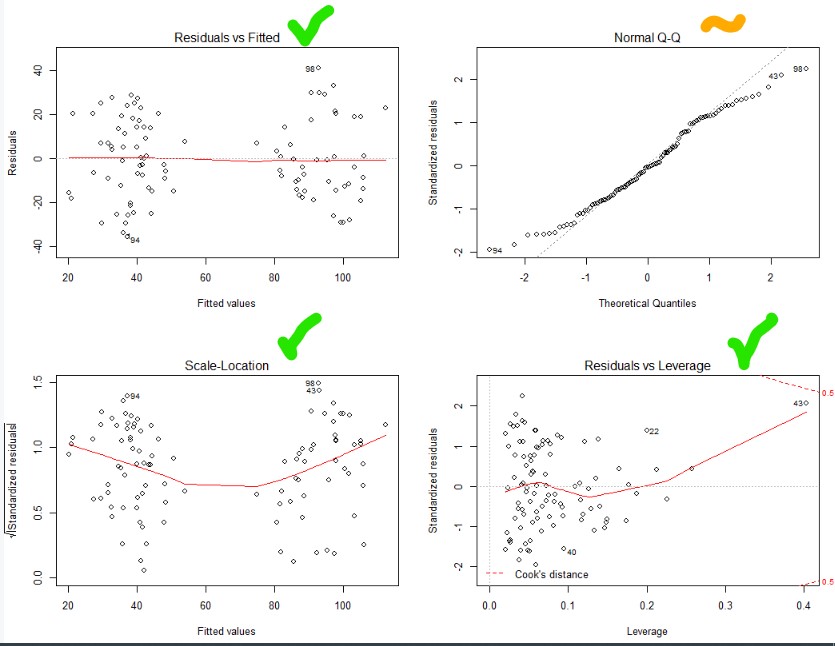

Top and bottom left – nice and flat. Heteroskedastic and no relationship between fitted value and the variability. Nice

Bottom right – no outliers (you’ll see dots outside of the dotted line, if their were)

Top right – ideally all the dots are on the line (normally distributed). So let’s try a better transformation of our dependent variable using a BoxCox transformation!

Box-Cox transformation!

The Box-Cox transformation is where the Box-Cox algorithm works out the best transformation to achieve normality.

First run the stepwise model as above but with the un-transformed variable. Then run the final model through the Box-Cox algorithm setting the potential lamba (power) to between -5 and 5. Lambda is the power that you are going to raise your dependent variable to.

Box-Cox algorithm will essentially run the model and score the normality over and over again. Each time transforming the dependent variable to every power between -5 and 5 going in steps on 0.001. The optimal power is where the normality reaches its maximum. So you then create the variable “Selected.Power” where the normality score was at it’s max. You then raise your dependent variable to that power and run your models again!

#BoxCox transformation
full.model.untransformed<-lm(Inflammation ~ Age*Sex*Blood.pressure*Infection*Bacterial.count, data = dat)
step.model.untransformed<-stepAIC(full.model, direction="both", trace = F)

boxcox<-boxcox(step.model.untransformed,lambda = seq(-5, 5, 1/1000),plotit = TRUE )
Selected.Power<-boxcox$x[boxcox$y==max(boxcox$y)]
Selected.Power
> 0.536

dat$inflammation.boxcox.transformed<-dat$Inflammation^Selected.Power

The Box-Cox algorithm chose 0.536, which is really close to a square-root transformation. But this minor difference does effect the distribution of the residuals.

 

#Running again with BoxCox transformed variable
#Set up full model
full.model<-lm(inflammation.boxcox.transformed ~ Age*Sex*Blood.pressure*Infection*Bacterial.count, data = dat)

#Perform stepwise regression in both directions
step.model<-stepAIC(full.model, direction="both", trace = F)

summary(step.model)


#Checking assumptions 
par(mfrow=c(2,2)) 
plot(step.model)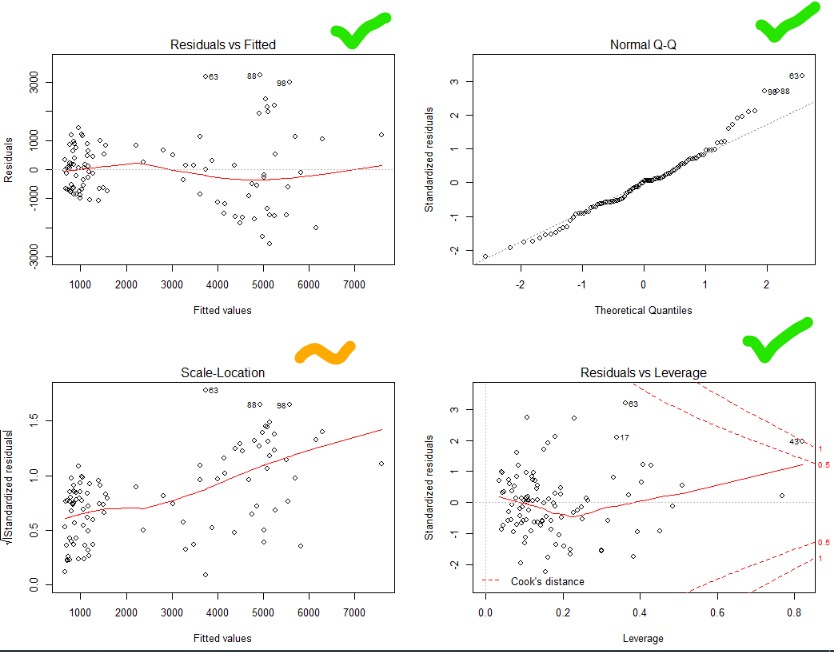

Top right – Yes that is pretty good. Normality achieved!

Top and bottom left – Ok, not great. Things get a bit more variable as the predicted values go up. Guess you can’t win them all.

Bottom right – no outliers beyond the dotted line (1). Though one is close.